**NVIDIA Vulkan Compute Mipmaps Sample**
**Algorithm Details**
Authors: David Zhao Akeley
This document describes the cache-aware parallelization strategy used
by `nvpro_pyramid`.
# Introduction
The basic observation of this project is that the outputs for one mip
level can immediately be used as inputs for generating the next mip level.
For example, in the power-of-two case, a 64x64 tile of the base mip level
becomes a 32x32 tile in level 1, which can immediately be used to calculate
a 16x16 tile in level 2, then an 8x8 tile in level 3, and so on.
This observation allows us to:
* Generate multiple levels in a single dispatch, minimizing
synchronization overhead (i.e. 1 barrier per N levels, rather than 1
barrier per 1 level).
* Use samples as inputs immediately after they are generated, keeping
them in register or L1 cache storage, rather than round-tripping to
L2 or main memory.
The situation is a bit less clean for the general (NP2) case, to be
discussed later, but the basic principle still applies.
To keep expectations realistic: in a full mip pyramid, 75% of the data
is in the base mip level, which inevitably must be read from main
memory. So, any cache awareness only targets inefficiency in the
remaining 25% of the mip pyramid. The benefits of this are measurable,
but won't be orders-of-magnitude better.
# Background
The reader is expected to understand compute shaders, shared memory
and
[`barrier()`](https://www.khronos.org/registry/OpenGL-Refpages/gl4/html/barrier.xhtml),
and [Vulkan 1.1 subgroup shuffle
operations](https://www.khronos.org/blog/vulkan-subgroup-tutorial)
(a.k.a. warp shuffles).
# Two Pipelines
Because of the simplicity of the power-of-2 case (= lower resource
consumption needed), this library provides two pipelines: a "fast
pipeline" motivated by the need to handle the power-of-2 case as
efficiently as possible, and a more resource-hungry "general pipeline"
fallback.
The `fastPipeline` shader (`NVPRO_PYRAMID_IS_FAST_PIPELINE != 0`) is
specialized for the case where the input level has even dimensions and
subgroup shuffle operations are available. It can generate from 1
to 6 mip levels (call this $M$) and requires that the input level
be evenly divisible into tiles of size $2^M \times 2^M$.
The `generalPipeline` shader (`NVPRO_PYRAMID_IS_FAST_PIPELINE == 0`)
is used when the `fastPipeline`'s requirements are not met (either due
to an odd input mip level size, or missing device features). Note in
particular that this is the only shader that needs code for handling
non-2x2 kernels.
Generating all mip levels in a single pass is an explicit *non-goal*
of this library: if there are more mip levels to be generated than can
be filled by a single dispatch, the library handles as many levels as
it can, records a barrier command, then issues more dispatches until
all levels are (scheduled to be) filled. One nice consequence of this
is that the fast pipeline can be used outside of its original
power-of-2 use case: if the base mip level has even dimensions (but
not necessarily a power-of-2), the fast pipeline can be used to
generate the first few mip levels (where the bulk of the data lies),
with the general pipeline only being used to fill in the comparatively
tiny "cap" of the mipmap pyramid. For example:
* Image size 1920x1080: Divide into 8x8 tiles, fill the first 3 levels
using `fastPipeline`, then switch to `generalPipeline`.
* Image size 2560x1440: Divide into 32x32 tiles, fill the first 5 levels
using `fastPipeline`, then switch to `generalPipeline`.
In the following descriptions, let $L$ be the mip level of the
dispatch's input mip level.
# Fast Pipeline
This section will begin by describing how the fast pipeline handles
filling just one mip level ($M = 1$) then build up to $M = 6$. Each
tile is assigned to a "team" of threads, with the team size dependent
on the input tile size, $(2^M, 2^M)$.
## 1 Level
Degenerate case, each thread loads and reduces 4 samples (or uses
hardware sampler filtering), and stores the resulting sample to level
$L + 1$. Note that this path of the shader is not actually used by
default, as handling only one level reduced performance in practice.
## 2 Levels
Suppose that the input mip level can be split into 4x4 tiles and we
want to generate 2 mip levels in this dispatch. Divide the dispatched
threads into teams of 4 and assign one tile to each thread. For level
$L + 1$, each thread is assigned a sample to generate for the 2x2
output tile, using the pattern
```text
+---+---+ +--
| 0 | 1 | | 0
+---+---+ +--
| 2 | 3 | | 2
+---+---+ +--
+---+---+ +--
| 0 | 1 | | 0 (neighboring tiles)
```
Once this is done, the 0th thread in each team uses `subgroupShuffleXor` with
masks 1, 2, and 3 to get the samples generated by the other threads in the
team, and reduces these samples, plus its own sample, to generate the
assigned 1x1 sample in level $L+2$. (The remaining threads are idle.)
```text
input level
+-------+ +---+---+ +-------+
| | | 0 | 1 | | |
| 4x4 | ====> +---+---+ ====> | 0 |
| | | 2 | 3 | | |
+-------+ +---+---+ +-------+
```
## 3 Levels
This above 2x2 tile is the basic tiling pattern for the pipeline. We
can apply the pattern recursively to handle additional mip levels. To
handle an 8x8 input tile and generate 3 mip levels, we can pack
together 4 sub-teams into a team of 16 like so:
```text
+---+---++---+---+
| 0 | 1 || 4 | 5 |
+---+---++---+---+
| 2 | 3 || 6 | 7 |
+===+===++===+===+
| 8 | 9 ||12 |13 |
+---+---++---+---+
|10 |11 ||14 |15 |
+---+---++---+---+
```
Each sub-team of 4 threads uses the earlier algorithm to fill levels
$L + 1$ and $L + 2$. Notice how nicely `subgroupShuffleXor` adapts to
the recursion (and to different subgroup sizes, so long as the
subgroup is not smaller than the team size).
```text
input level (L) level L+1 level L+2
+---------------+ +---+---++---+---+ +-------++-------+
| | | 0 | 1 || 4 | 5 | | || |
| | +---+---++---+---+ | 0 || 4 |
| | | 2 | 3 || 6 | 7 | | || |
| 8x8 | ====> +===+===++===+===+ ====> +=======++=======+
| | | 8 | 9 ||12 |13 | | || |
| | +---+---++---+---+ | 8 || 12 |
| | |10 |11 ||14 |15 | | || |
+---------------+ +---+---++---+---+ +-------++-------+
```
Once the first two generated mip levels are filled, the 0th thread in
each team shuffles using masks 4, 8, and 12 to get the 3 neighboring
samples, and reduces these together with its own sample to form the
sole 1x1 sample in level $L + 3$.
```text
input level (L) level L+1 level L+2 level L+3
+---------------+ +---+---++---+---+ +-------++-------+ +---------------+
| | | 0 | 1 || 4 | 5 | | || | | |
| | +---+---++---+---+ | 0 || 4 | | |
| | | 2 | 3 || 6 | 7 | | || | | |
| 8x8 | ====> +===+===++===+===+ ====> +=======++=======+ ====> | 0 |
| | | 8 | 9 ||12 |13 | | || | | |
| | +---+---++---+---+ | 8 || 12 | | |
| | |10 |11 ||14 |15 | | || | | |
+---------------+ +---+---++---+---+ +-------++-------+ +---------------+
```
For additional clarity, the same 8x8 -> 1x1 reduction algorithm is depicted
again here, juxtaposed with a diagram of shuffles and active/idle threads.
**************************************************************************************
*+-+-+-+-+-+-+-+-+ input level (L), 8x8 tile assigned to 16-thread team *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
*+-+-+-+-+-+-+-+-+ *
* v *
* | *
*+---+---+---+---+ level L+1 (4x4) *
*| 0 | 1 | 4 | 5 | *
*+---+---+---+---+ *
*| 2 | 3 | 6 | 7 | +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+*
*+---+---+---+---+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |10 |11 |12 |13 |14 |15 |*
*| 8 | 9 |12 |13 | +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+*
*+---+---+---+---+ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ *
*|10 |11 |14 |15 | | | | | | | | | | | | | | | | | *
*+---+---+---+---+ +---+---+---+ | | | | +---+---+---+ | | | | *
* v | | | | | | | | | | *
* | | | | | | | xor 1, 2, 3 | | | | *
*+-------+-------+ level L+2 (2x2) +---+---+---+ | +---+---+---+ *
*| | | | | | | *
*| 0 | 4 | v v v v *
*| | | +---+ +---+ +---+ +---+ *
*+-------+-------+ | 0 | x x x | 4 | x x x | 8 | x x x |12 | x x x *
*| | | +---+ +---+ +---+ +---+ *
*| 8 | 12 | ^ ^ ^ ^ *
*| | | | | | | *
*+-------+-------+ | | | | *
* v +---------------+---------------+---------------+ *
* | | *
*+-------+-------+ level L+3 (1x1) xor 4, 8, 12 *
*| | | *
*| | v *
*| | +---+ *
*| 0 | | 0 | x x x x x x x x x x x x x x x *
*| | +---+ *
*| | *
*| | *
*+-------+-------+ *
**************************************************************************************
!!! NOTE
Given a warp size of 32 threads, each warp is actually running 2
such reduction algorithms, split between the low and high 16 threads.
## 4 or 5 Levels (Shared Memory)
This recursive pattern can, in theory, continue indefinitely. For
example, to handle a 16x16 input tile and generate 4 mip levels, we
could execute the 3-level algorithm with 4 sub-teams of size 16, and
then have the 0th thread (out of the team of 64) shuffle using masks
16, 32, 48 to get the data to generate the 1x1 sample of level $L+4$.
However, this recursion is bounded in practice by the subgroup size; this
4-mip-level algorithm won't work for NVIDIA cards (subgroup size 32);
xor-shuffling with masks 32 or 48 will yield undefined values.
The threads use shared memory to communicate in this case. This is not
as performant as shuffles, as communication is through cache memory,
not registers, and requires explicit `barrier()` synchronization
(wheras subgroups are naturally synchronized), but is still an
improvement over communicating between dispatches through main GPU
memory.
For generating 4 mip levels of a 16x16 input tile with a team of 64
threads, we divide the team into 4 sub-teams, each running the
3-levels algorithm. The 0th thread in each sub-team, in addition to
writing its sample to level $L+3$, also writes its sample to one
quadrant of a 2x2 tile in shared memory. Issue a barrier, then, the
0th thread of the whole team of 64 reads the 2x2 tile in shared memory
and reduces it to form the 1x1 level of level $L+4$.
For generating 5 mip levels, shared memory instead holds a 4x4 tile
for the team. Divide the team of 256 threads into 16 sub-teams, and
the input 32x32 tile into 8x8 sub-tiles. Generate the resulting tiles
in levels $L+1$ through $L+3$ for each 8x8 input sub-tile. Issue a
barrier, then nominate 4 threads out of the team to run the 2-level
algorithm, taking inputs from shared memory. This fills the 2x2 and
1x1 tiles of level $L+4$ and $L+5$, respectively.
```text
input level (L) level L+3 (+ copy in smem) level L+4 level L+5
+---+---++---+---+ +---+---++---+---+ +-------++-------+ +---------------+
|8x8|8x8||8x8|8x8| | 0| 16|| 64| 80| | || | | |
+---+---++---+---+ +---+---++---+---+ | 0 || 1 | | |
|8x8|8x8||8x8|8x8| | 32| 48|| 96|112| | || | | |
+===+===++===+===+ => omitted => +===+===++===+===+ ==|==> +=======++=======+ ====> | 0 |
|8x8|8x8||8x8|8x8| | |128|144||192|208| | | || | | |
+---+---++---+---+ | +---+---++---+---+ | | 2 || 3 | | |
|8x8|8x8||8x8|8x8| | |160|176||224|240| | | || | | |
+---+---++---+---+ | +---+---++---+---+ | +-------++-------+ +---------------+
16-thread team handles each 8x8 sub-tile (barrier)
```
## 6 Levels
Since we already assume a subgroup size of at least 16, we could adapt
this algorithm to handle a 64x64 input tile and fill 6 mip levels in
one dispatch, by using the 3-layer algorithm to reduce to an 8x8 tile
in shared memory, then generate 3 more layers using the same
algorithm, using shared memory as input.
Unfortunately, this doesn't perform well in practice, as it requires a
team size (and therefore, a workgroup size) of 1024 threads, which
turned out to be suboptimal. Since extending the algorithm at the end
is no longer a practical option, we instead generate an extra level at
the beginning, and reduce to the five layer case.
The plan is to apply the 5-levels algorithm using level $L+1$ as
input, generating levels $L+2$ through $L+6$ (with the tile in level
$L+4$ communicated through shared memory). Each thread in the team is
assigned 1 sample in level $L+2$ to generate; this requires 4 input
samples from level $L+1$. So to make it work, just have each thread
generate and write the 4 samples it needs from level $L+1$, using 16
samples from level $L$ as input. The situation looks like:
```text
64x64 32x32 16x16 8x8 4x4
Level L+4
input level (L) level L+1 level L+2 level L+3 (+ copy in smem)
+---------------+-- +---+---+---+---+-- +-------+-------+-- +---------------+-- +-----------------
| | | 0 | 0 | 1 | 1 | 4 | | | | | |
| | +---+---+---+---+-- | 0 | 1 | 4 | | | 0
| | | 0 | 0 | 1 | 1 | 4 | | | | | |
| 8x8 | ====> +---+---+---+---+ ====> +-------+-------+ ====> | 0 | ====> |
| sub-tile | | 2 | 2 | 3 | 3 | 6 | | | | | |
| | +---+---+---+---+-- | 2 | 3 | 6 | | |
| | | 2 | 2 | 3 | 3 | 6 | | | | | | ===>
+---------------+-- +---+---+---+---+-- +-------+-------+-- +---------------+-- | (continues
| | | 8 | 8 | 9 | 9 | 12 | 8 | 9 | 12 | 8 | 12 | to L+6)
```
Squeezing out an extra 6th level for the fast pipeline turned out to
be a worthwhile optimization for images of size 2048x2048 and
4096x4096; both sizes would require 3 dispatches to generate if only 5
levels could be filled per dispatch, versus only 2 dispatches for 6
levels per dispatch. However, when only 5 or fewer mip levels are eligible
to be generated, this trick instead reduced performance, so, we only use
this extra "generate the 4 samples you need" step when generating 6 levels;
the 1 to 5 level cases are still handled as described earlier.
# Fast Pipeline Performance
This section justifies the use of these optimizations and quantifies
their effects.
These results come from the built-in benchmarking utility of the demo
app. This benchmarking utility runs each algorithm multiple times in
several batches, and reports the minimum and median GPU runtime of the
batches. Generally, the minimum time seems most consistent (and
therefore most reliable for comparison purposes).
**Runtimes are from testing on an RTX 3090 card, reported in
nanoseconds, with the minimum runtime above the median. The relative
runtime compared to the blit algorithm is parenthesized.**
!!! NOTE
[Remarks on Test Images](./test_images.txt)
## Blit Comparison
This table compares the default `nvpro_pyramid` shader with the
typical blit mipmap generation method on a variety of image sizes.
To control for the cost of blit (graphics) vs compute workloads,
there is also a comparison with a `onelevel` compute shader that
handles only 1 level per dispatch.
Note that the `onelevel` shader is not an exact substitute for blits
in the non-power-of-2 case, due to the 3x3 kernel.
***********************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | blit | onelevel |*
*+----------------+----------------+----------------+----------------+*
*| 1920,1080 | 36736 ( 80.6%)| 45568 (100.0%)| 46080 (101.1%)|*
*| | 37632 ( 80.8%)| 46592 (100.0%)| 46848 (100.5%)|*
*+----------------+----------------+----------------+----------------+*
*| 2560,1440 | 43008 ( 72.3%)| 59520 (100.0%)| 60672 (101.9%)|*
*| | 43648 ( 72.1%)| 60544 (100.0%)| 61440 (101.5%)|*
*+----------------+----------------+----------------+----------------+*
*| 3840,2160 | 75520 ( 80.3%)| 94080 (100.0%)| 96000 (102.0%)|*
*| | 76288 ( 80.0%)| 95360 (100.0%)| 96768 (101.5%)|*
*+----------------+----------------+----------------+----------------+*
*| 2048,2048 | 35712 ( 57.2%)| 62464 (100.0%)| 62748 (100.5%)|*
*| | 36480 ( 57.3%)| 63616 (100.0%)| 63488 ( 99.8%)|*
*+----------------+----------------+----------------+----------------+*
*| 4096,4096 | 112000 ( 70.1%)| 159744 (100.0%)| 159232 ( 99.7%)|*
*| | 113024 ( 70.2%)| 161024 (100.0%)| 160128 ( 99.4%)|*
*+----------------+----------------+----------------+----------------+*
***********************************************************************
!!! NOTE
See `demo_app/rtx3090.json` for complete timing data.
To get a build for reproducing these results, run CMake with
`-DPIPELINE_ALTERNATIVES=1`.
The slowdown for the blit algorithm can clearly be seen in this
[NSight GPU
Trace](https://docs.nvidia.com/nsight-graphics/UserGuide/#gpu_trace_0):
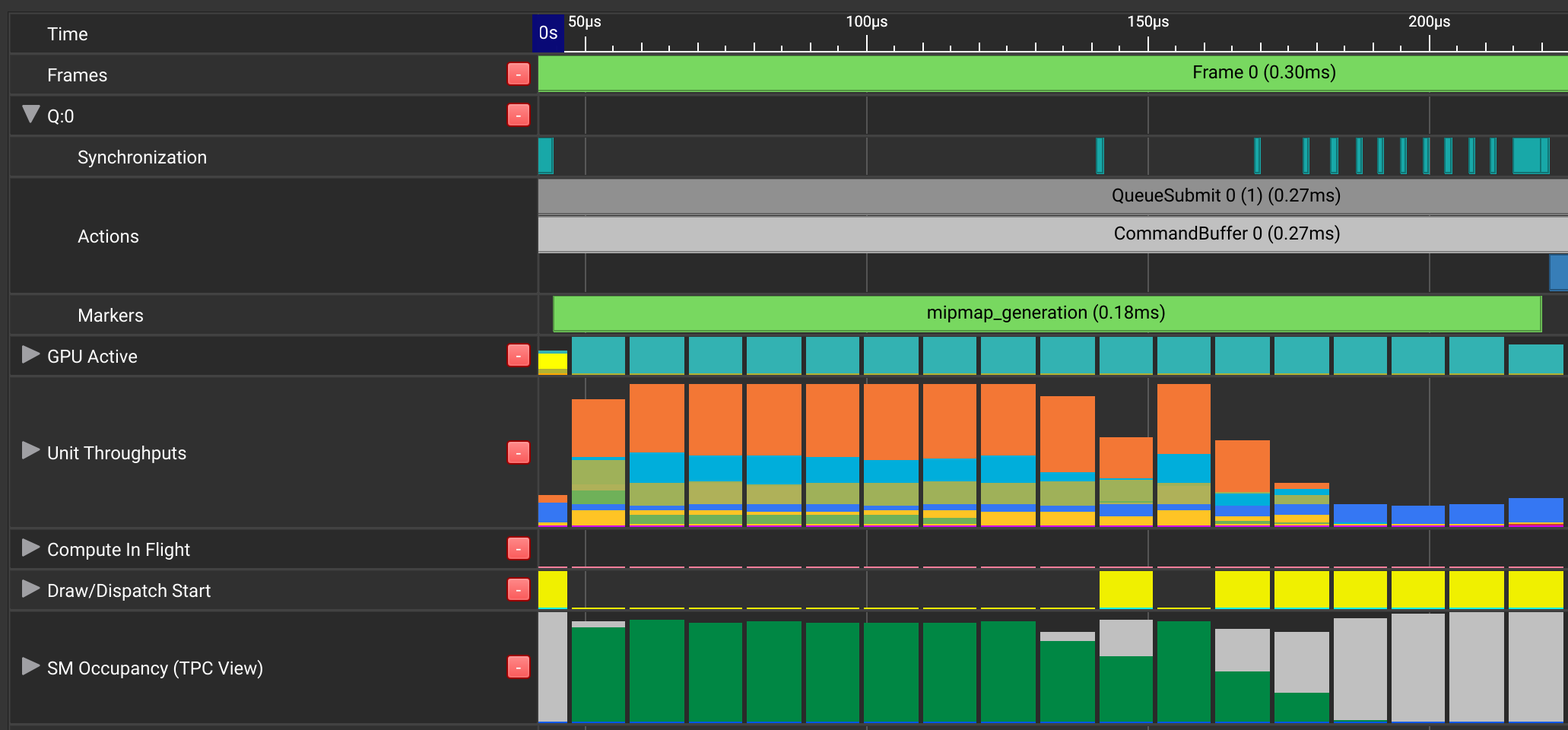
It's apparent that there's a large "dead zone" of low GPU utilization
towards the end of the `mipmap_generation` section, associated with
the many synchronization points visible at the top. Throughput and SM
Occupancy (green) drop to almost zero at the end, with an additional
dip between the first two blits.
In contrast, this GPU Trace of the default `nvpro_pyramid` shader
shows more efficient utilization. (Compute SM occupancy now in orange.)
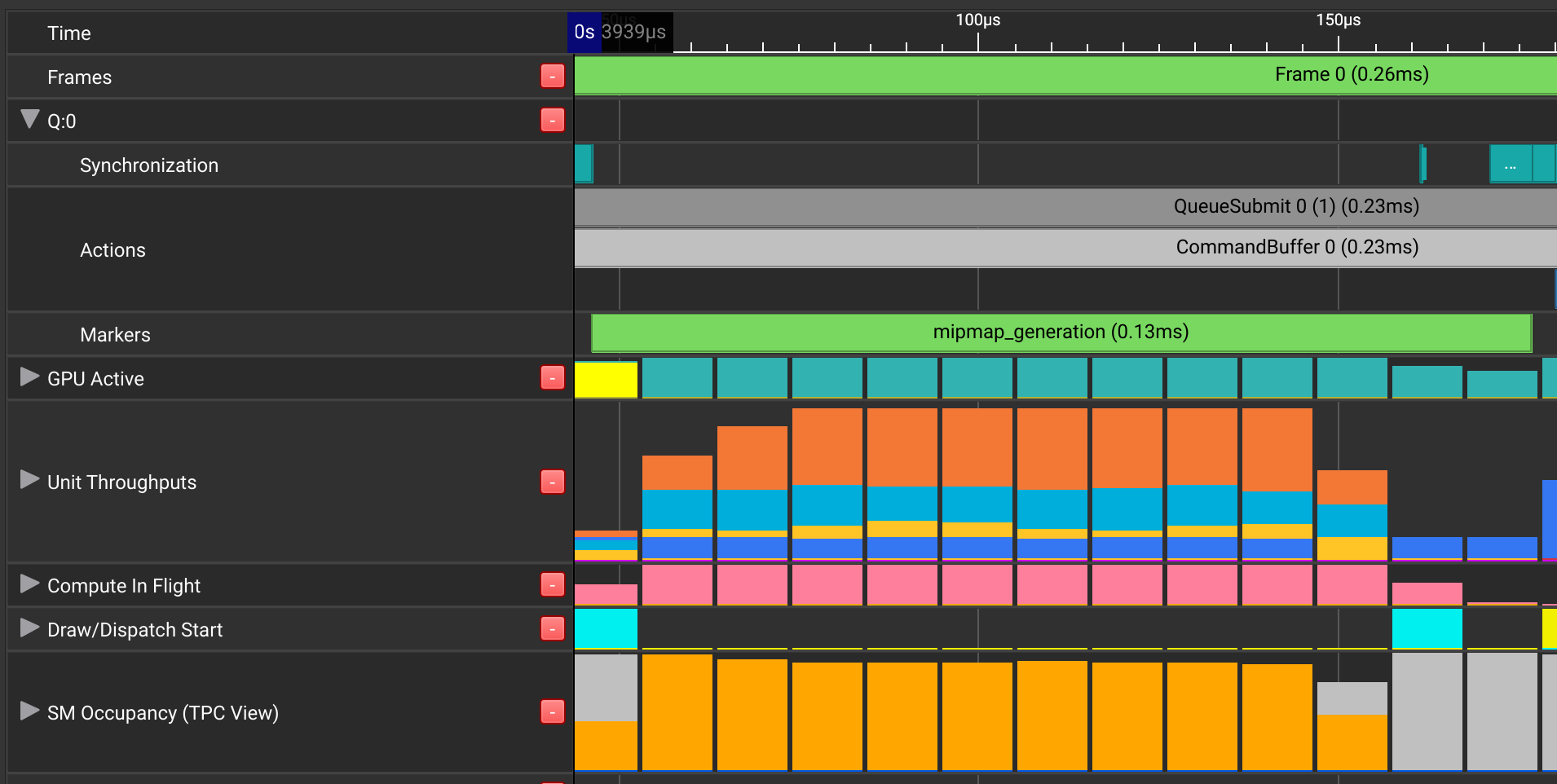
!!! NOTE
To enable these debug markers, run CMake with `-DUSE_DEBUG_UTILS=ON`.
## 1 or 6 Levels
This table isolates effects at the low and high end of the number of
generated levels per dispatch. The default `nvpro_pyramid` shader is
only dispatched for between 2 and 6 generated levels, requiring at a
minimum that the input level to be evenly divisible into 4x4 tiles.
The `levels_1_6` shader relaxes the divisibility requirement to 2x2,
which allows for only 1 level to be generated in the worst case.
The `levels_1_5` shader removes support for generating 6 levels
in a single dispatch; this means the shader never exercises
the special case 6-level behavior described earlier.
The `workgroup1024` shader tests the alternate proposal for generating
6 levels per dispatch, which expands the workgroup size to 1024
threads.
****************************************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | levels_1_6 | levels_1_5 | workgroup1024 |*
*+----------------+----------------+----------------+----------------+----------------+*
*| 1920,1080 | 36736 ( 80.6%)| 36224 ( 79.5%)| 36096 ( 79.2%)| 39808 ( 87.4%)|*
*| | 37632 ( 80.8%)| 37376 ( 80.2%)| 37376 ( 80.2%)| 40704 ( 87.4%)|*
*+----------------+----------------+----------------+----------------+----------------+*
*| 2560,1440 | 43008 ( 72.3%)| 42752 ( 71.8%)| 42752 ( 71.8%)| 49664 ( 83.4%)|*
*| | 43648 ( 72.1%)| 43276 ( 71.5%)| 43264 ( 71.5%)| 50688 ( 83.7%)|*
*+----------------+----------------+----------------+----------------+----------------+*
*| 3840,2160 | 75520 ( 80.3%)| 75292 ( 80.0%)| 75392 ( 80.1%)| 88204 ( 93.8%)|*
*| | 76288 ( 80.0%)| 76160 ( 79.9%)| 76416 ( 80.1%)| 90752 ( 95.2%)|*
*+----------------+----------------+----------------+----------------+----------------+*
*| 2048,2048 | 35712 ( 57.2%)| 35584 ( 57.0%)| 37760 ( 60.5%)| 43008 ( 68.9%)|*
*| | 36480 ( 57.3%)| 36480 ( 57.3%)| 38144 ( 60.0%)| 44032 ( 69.2%)|*
*+----------------+----------------+----------------+----------------+----------------+*
*| 4096,4096 | 112000 ( 70.1%)| 112000 ( 70.1%)| 112640 ( 70.5%)| 139008 ( 87.0%)|*
*| | 113024 ( 70.2%)| 112904 ( 70.1%)| 114432 ( 71.1%)| 142720 ( 88.6%)|*
*+----------------+----------------+----------------+----------------+----------------+*
*| 4094,4094 | 161664 (102.4%)| 168448 (106.6%)| 168576 (106.7%)| 169088 (107.1%)|*
*| | 163840 (102.8%)| 169600 (106.4%)| 169472 (106.3%)| 170496 (107.0%)|*
*+----------------+----------------+----------------+----------------+----------------+*
****************************************************************************************
Except for the 1024-thread workgroup shader, which is bad for
performance in all cases, the effects of these level changes can only
be seen for specific image sizes.
The `levels_1_6` shader has notably worse performance on the 4094x4094
image, which is evenly divisible into 2x2 tiles but not 4x4. The
general pipeline (to be discussed) handles 2 levels per dispatch,
thus, using the fast pipeline to handle only 1 level (the 4094x4094 to
2047x2047 reduction) naturally has worse performance compared to the
`default` shader's behavior of leaving the entire generation to the
general pipeline.
The `levels_1_5` shader only shows a significant loss compared to the
default (6 level) shader on the 2048x2048 image size, which requires
three dispatches with the alternate shader compared to two with the
default. This confirms the usefulness of the 6-level optimization,
although the effect is small enough to make that a micro-optimization
at best.
Curiously, the performance loss for the 4096x4096 case is small enough
to be within the bounds of measurement error (note the overlapped
min/median ranges), even though eliminating 6-level support also
converts that from a 2-dispatch case to a 3-dispatch case. Meanwhile,
the non-power-of-2 cases show no response to eliminating 6-level
support, which is expected, as none of those images meet the 64x64
divisibility requirements needed to exercise that code path.
## Shared Memory
This table demonstrates the effect of eliminating shared memory in the
fast pipeline (and thus capping the maximum number of levels filled
per dispatch to 3, instead of 6).
******************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | levels_1_3 |*
*+----------------+----------------+----------------+*
*| 1920,1080 | 36736 ( 80.6%)| 36480 ( 80.1%)|*
*| | 37632 ( 80.8%)| 37376 ( 80.2%)|*
*+----------------+----------------+----------------+*
*| 2560,1440 | 43008 ( 72.3%)| 45392 ( 76.3%)|*
*| | 43648 ( 72.1%)| 45824 ( 75.7%)|*
*+----------------+----------------+----------------+*
*| 3840,2160 | 75520 ( 80.3%)| 78084 ( 83.0%)|*
*| | 76288 ( 80.0%)| 78848 ( 82.7%)|*
*+----------------+----------------+----------------+*
*| 2048,2048 | 35712 ( 57.2%)| 40320 ( 64.5%)|*
*| | 36480 ( 57.3%)| 40832 ( 64.2%)|*
*+----------------+----------------+----------------+*
*| 4096,4096 | 112000 ( 70.1%)| 116480 ( 72.9%)|*
*| | 113024 ( 70.2%)| 117760 ( 73.1%)|*
*+----------------+----------------+----------------+*
******************************************************
We see that the `levels_1_3` shader shows the most notable losses for
the power-of-2 image sizes, which otherwise could have been filled
with much fewer dispatches. The (minor) expense of handling shared
memory in the default shader appears to be completely offset by
performance gains. The 2560x1440 and 3840x2160 image sizes also
show some performance loss, as those image sizes could have their
initial 5 or 4 levels (respectively) handled by the default shader
compared to only 3 for the alternative.
!!! NOTE
The `levels_1_3` case uses a different shader than the `default` case,
instead of merely re-using the default shader with different
dispatch parameters. Thus the shared memory is really removed,
not simply unused.
## Bilinear Filter
This table demonstrates the importance of taking advantage of hardware
bilinear sampling, via the `NVPRO_PYRAMID_LOAD_REDUCE4` macro. The
`noBilinear` shader is identical to the default one, except that
manual load-and-average-4-samples shader code is substituted wherever
a sampler would otherwise have been used.
***********************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | noBilinear | blit |*
*+----------------+----------------+----------------+----------------+*
*| 1920,1080 | 36736 ( 80.6%)| 36992 ( 81.2%)| 45568 (100.0%)|*
*| | 37632 ( 80.8%)| 37760 ( 81.0%)| 46592 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 2560,1440 | 43008 ( 72.3%)| 44416 ( 74.6%)| 59520 (100.0%)|*
*| | 43648 ( 72.1%)| 45184 ( 74.6%)| 60544 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 3840,2160 | 75520 ( 80.3%)| 76928 ( 81.8%)| 94080 (100.0%)|*
*| | 76288 ( 80.0%)| 78336 ( 82.1%)| 95360 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 2048,2048 | 35712 ( 57.2%)| 47104 ( 75.4%)| 62464 (100.0%)|*
*| | 36480 ( 57.3%)| 47872 ( 75.3%)| 63616 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 4096,4096 | 112000 ( 70.1%)| 140800 ( 88.1%)| 159744 (100.0%)|*
*| | 113024 ( 70.2%)| 144384 ( 89.7%)| 161024 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
***********************************************************************
For the power-of-2 cases, this manual filtering erases much of the
gains that the compute shader has over the blit method. The
non-power-of-2 cases are less sensitive to hardware sampler
optimization, presumably because many of the layers are handled by the
general pipeline, which must handle the general 3x3 kernel case and
cannot (easily) leverage hardware sampling anyway.
# General Pipeline
The general pipeline handles any input image size. Each dispatch
generates up to 2 mip levels.
## Kernel Background
The mathematical methods for non-power-of-2 mipmap generation are
taken from NVIDIA's ["Technical Report: Non-Power-of-Two Mipmap
Creation"](http://download.nvidia.com/developer/Papers/2005/NP2_Mipmapping/NP2_Mipmap_Creation.pdf).
The techincal details are very outdated (e.g. ARB assembly
programming) but the math is still applicable. The kernel size for
generating level $N+1$ from $N$ can range anywhere from $1 \times 1$
to $3 \times 3$, excluding $1 \times 1$ itself, with the kernel
weights chosen so that mipmap generation is "energy conserving".
If level $N$ has size $(D_0, D_1$), then the kernel size for generating
level $N+1$, $(k_0, k_1)$, is given by
$$
k_i = \begin{cases}
1 & D_i = 1 \\
2 & D_i \text{ even} \\
3 & D_i \text{ odd and } D_i \ne 1
\end{cases}
$$
## The Complication
One nice property of power-of-2 textures, which the fast pipeline
implicitly depends on, is that each sample of the mipmap is used as
input for only one sample in the next mip level. This makes it easy to
partition the input into self-contained tiles.
Unfortunately, this property no longer holds in the non-power-of-2 case.
For example, reducing a 5x5 mip level to the next 2x2 mip level requires
some input samples to be consumed 2 or 4 times:
```text
+---+---+---+---+---+ +---------+---------+
| | | 2 | | | | | |
+---+---+---+---+---+ | | |
| | | 2 | | | | | |
+---+---+---+---+---+ | | |
| 2 | 2 | 4 | 2 | 2 | =====> +---------+---------+ (each sample generated with 3x3 kernel)
+---+---+---+---+---+ | | |
| | | 2 | | | | | |
+---+---+---+---+---+ | | |
| | | 2 | | | | | |
+---+---+---+---+---+ +---------+---------+
```
Suppose level $L+2$ is split into tiles that are each assigned to a
team. Each team has to generate (or peek at) all the samples in level
$L+1$ that are needed as input for its level-$L+2$ tile. Since some of
these samples are shared, the teams have to either
* find a way to divide the work for the shared samples and
communicate the results to each other, or
* independently generate the shared samples (not work-efficient
w.r.t. $n =$ mip levels)
The general pipeline accepts the latter approach; the
work-inefficiency was outweighed in practice by improved cache and
synchronization performance, up to a point.
## 1 Level
The 1-level case is identical to that of the fast pipeline (1 thread
per sample generated), except that it's possible for 2x3, 3x2, or 3x3
kernels to be used.
## 2 Levels
This is a bit easier to explain by working backwards.
In the 2-level case, level $L+2$ is broken into $D \times D$ tiles,
each assigned to a seperate workgroup of $W$ threads ($D, W$ to be
determined). The shader does manual bounds checking to handle tiles at
the edge that may exceed the bounds of the image. To generate this
tile, the workgroup has to generate a tile of level $L+1$ of a size
ranging from $(1 \times 1)$ to $(2D + 1 \times 2D + 1)$, depending on
the kernel size (i.e. depending on the parity of level $L+1$'s
dimensions). This requires as input somewhere from a size $(1 \times
1)$ to $(4D + 3 \times 4D + 3)$ tile of level $L$.
The full algorithm, then, is
* Calculate the needed size of the level $L+1$ tile based on the
kernel size for the $L+1$ to $L+2$ step.
* Cooperatively calculate and write the needed tile for level $L+1$;
also cache this in shared memory.
* Issue a barrier.
* Cooperatively calculate and write the assigned level $L+2$ tile,
using inputs from shared memory.
## Parameter Tuning
A Python script was used to generate many different combinations of
$T$ and $D$, above. The parameters ultimately chosen were $T = 128$
threads and an output tile edge length of $D = 8$. Therefore the
maximum size of the level $L + 1$ tile in shared memory is $17 \times 17$.
## 3+ Levels [not implemented]
Experiments in handling 3 levels in a single general pipeline dispatch
did not yield promising results. It's possible that the redundant work
at this point outweighed any potential cache benefits; note that the
amount of redundant work increases quadratically with the number of
mip levels generated: if we break the final output level $N$ into $D
\times D$ tiles, each assigned to a team, then, in the worst-case $3
\times 3$ kernel case, each team generates
* a $(2D + 1, 2D + 1)$ tile of level $N-1$, offset by $2D$ from
neighboring teams' tiles, with $1$ sample of overlap per row/column.
* a $(4D + 3, 4D + 3)$ tile of level $N-2$, offset by $4D$ from
neighboring teams' tiles, with $3$ samples of overlap per row/column.
* a $(8D + 7, 8D + 7)$ tile of level $N-3$, offset by $8D$ from
neighboring teams' tiles, with $7$ samples of overlap per row/column.
* and so on...
# General Pipeline Performance
The general pipeline does not have as clear a performance advantage
over the standard blit algorithm compared to the fast pipeline,
because
* The general pipeline does more work, using an up-to-3x3 kernel in
shader code vs hardware bilinear filtering (2x2 kernel) for the blit
* The general pipeline requires a barrier every 2 dispatches.
Nevertheless, because of the hybrid fast/general pipeline approach, in
many cases the `nvpro_pyramid` library still outperforms blits, while
also generating an aesthetically higher-quality result (generate
benchmark results and compare `default` with `blit`). To isolate the
general-case comparison, we used the `generalblit` algorithm, which
only used blits to substitute for general pipeline
dispatches. (i.e. both `generalblit` and `default` use the same fast
pipeline when the needed divisibility is satisfied). Even in this
case, the `nvpro_pyramid` library was still usually slightly faster or
on par with the blit speed.
***********************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | blit | generalblit |*
*+----------------+----------------+----------------+----------------+*
*| 1920,1080 | 36736 ( 80.6%)| 45568 (100.0%)| 42880 ( 94.1%)|*
*| | 37632 ( 80.8%)| 46592 (100.0%)| 43776 ( 94.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 2560,1440 | 43008 ( 72.3%)| 59520 (100.0%)| 50944 ( 85.6%)|*
*| | 43648 ( 72.1%)| 60544 (100.0%)| 51968 ( 85.8%)|*
*+----------------+----------------+----------------+----------------+*
*| 3840,2160 | 75520 ( 80.3%)| 94080 (100.0%)| 81664 ( 86.8%)|*
*| | 76288 ( 80.0%)| 95360 (100.0%)| 82816 ( 86.8%)|*
*+----------------+----------------+----------------+----------------+*
*| 2052,2052 | 44928 ( 71.6%)| 62720 (100.0%)| 49024 ( 78.2%)|*
*| | 45440 ( 71.3%)| 63744 (100.0%)| 49920 ( 78.3%)|*
*+----------------+----------------+----------------+----------------+*
***********************************************************************
It was only for the artificial test cases that frequently triggered
the worst-case 3x3 kernel that the standard blit approach was notably
faster:
***********************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+*
*| image size | nvpro_pyramid | blit | generalblit |*
*+----------------+----------------+----------------+----------------+*
*| 2047,2047 | 71592 (118.7%)| 60296 (100.0%)| 60800 (100.8%)|*
*| | 73088 (119.0%)| 61440 (100.0%)| 61952 (100.8%)|*
*+----------------+----------------+----------------+----------------+*
*| 4094,4094 | 161664 (102.4%)| 157952 (100.0%)| 158336 (100.2%)|*
*| | 163840 (102.8%)| 159360 (100.0%)| 159872 (100.3%)|*
*+----------------+----------------+----------------+----------------+*
*| 4095,4095 | 188032 (119.1%)| 157824 (100.0%)| 158336 (100.3%)|*
*| | 190464 (119.5%)| 159360 (100.0%)| 160000 (100.4%)|*
*+----------------+----------------+----------------+----------------+*
***********************************************************************
!!! TIP Benchmark Table Info
See [Fast Pipeline Performance](#fastpipelineperformance)
!!! NOTE
[Remarks on Test Images](./test_images.txt)
## Quality-Performance Tradeoff
For the test hardware and tested non-power-of-2 images, the worst case
performance degradation of the 3x3 kernel shader over blits was 20
percent. However, the amount of degradation is sensitive to hardware
and workload; there have been reports of worse degradation for other
hardware/image size combinations (not reproduced here).
In general, for non-power-of-2 images, **there is a non-trivial
quality-performance tradeoff**; the optimal decision depends on
the specific use case. The provided shader prioritizes quality at
the expense of performance; if this does not match the priorities of
the use case:
* Avoid non-power-of-2 images when practical.
* If unavoidable (e.g. for screenspace effects), consider downsampling
the image to the next-lowest power-of-2 size (e.g. 2560x1440 to
2048x1024) with the algorithm of your choice, then generate mipmaps
using the downsampled image. This isolates the performance and/or
quality penalty to only a single downsample, rather than
accumulating with each mip level.
# Baseline Comparison
!!! NOTE
See `demo_app/rtx3090_baseline.json`.
To get a build for reproducing these results, run CMake with
`-DPIPELINE_ALTERNATIVES=2`.
To get an idea of how close the shader is in speed to the theoretical
"speed-of-light" limiting speed, there is an extra `baseline` shader
that does not actually generate mipmaps, but simply reads all the
texels of the base mip level (using a hardware sampler), then writes
to all texels of subsequent mip levels, without any synchronization.
This is the bare mimimum amount of memory access needed to
successfully fill a mip pyramid, so, the difference in speed between
the `baseline` shader and an actual mipmap generation algorithm
represents arithmetic and/or synchronization overhead.
***********************************************************************
* key: nanosecond runtime (runtime relative to blit)*
* *
*+----------------+----------------+----------------+----------------+*
*| image size | baseline | nvpro_pyramid | blit |*
*+----------------+----------------+----------------+----------------+*
*| 1920,1080 | 18408 ( 41.6%)| 36100 ( 81.6%)| 44264 (100.0%)|*
*| | 18852 ( 42.1%)| 37040 ( 82.6%)| 44816 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 2560,1440 | 28228 ( 47.8%)| 42496 ( 71.9%)| 59084 (100.0%)|*
*| | 28760 ( 48.3%)| 42892 ( 72.0%)| 59600 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 3840,2160 | 56852 ( 60.5%)| 75196 ( 80.1%)| 93904 (100.0%)|*
*| | 57460 ( 60.8%)| 75736 ( 80.1%)| 94516 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 2048,2048 | 31264 ( 50.2%)| 35580 ( 57.1%)| 62312 (100.0%)|*
*| | 31696 ( 50.4%)| 36236 ( 57.6%)| 62884 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
*| 4096,4096 | 106196 ( 66.4%)| 112184 ( 70.2%)| 159884 (100.0%)|*
*| | 106956 ( 66.6%)| 112916 ( 70.3%)| 160544 (100.0%)|*
*+----------------+----------------+----------------+----------------+*
***********************************************************************
For the power-of-2 textures, the `nvpro_pyramid` shader is fairly
close in speed to the theoretical maximum. On the other hand, for
non-power-of-2, it's clear that substantial time is spent on the
(expensive) 3x3 kernel arithmetic and on additional
synchronization. It is an open question how to further optimize for
this case.